Պարապմունք 55

Թեմա՝ Բերված տեսքի քառակուսային հավասարումներ:

Առաջադրանքներ։

1․ Լուծել հավասարումները․

2․ Լուծել հավասարումները․

3․ Լուծել հավասարումները․

Պարապմունք 54

Թեմա՝ Ընդհանուր տեսքի քառակուսային հավասարումներ։

ax²+bx+c=0 տեսքի հավասարումը, որտեղ a -ն, b -ն և c -ն իրական թվեր են, և a≠0, կոչվում է քառակուսային հավասարում:

Քառակուսային հավասարման արմատները հաշվում են հետևյալ բանաձևերով՝

x₁=−b+√D/2⋅a,  x₂= −b−√D/2⋅a, որտեղ D=b²−4ac

D -ն անվանում են քառակուսային հավասարման  տարբերիչ  կամ դիսկրիմինանտ: 

Քառակուսային հավասարման արմատների գոյության հարցը և դրանց քանակը կախված D տարբերիչի արժեքից:

1) Եթե D<0 (բացասական է), ապա քառակուսային հավասարումը արմատներ չունի:

2) Եթե D=0, ապա քառակուսային հավասարումն ունի ճիշտ մեկ արմատ:

3) Եթե D>0 (դրական է), ապա քառակուսային հավասարումն ունի երկու իրարից տարբեր արմատներ:   

Օրինակ՝ Լուծենք հետևյալ քառակուսային հավասարումները՝

1) 3x²−5x+4=0

2)25x²−10x+1=0

3) x²−6x+5=0

4) 2x²−4x−3=0

Լուծումներ:

1) Հաշվենք 3x²−5x+4=0 հավասարման տարբերիչը՝ D=5²−4⋅3⋅4=25−48=−23<0

Պատասխան՝ հավասարումը արմատներ չունի:

2)Հաշվենք 25x²−10x+1=0 հավասարման տարբերիչը՝ D=10²−4⋅1⋅25=100−100=0

Հավասարումն ունի մեկ արմատ՝ x=−(−10)+√0/2⋅25=10/50=1/5=0.2

Պատասխան՝ x=0.2

3) Հաշվենք x²−6x+5=0 հավասարման տարբերիչը՝  D = (−6)² −4 ⋅1⋅5 =36−20=16>0

Հավասարումն ունի երկու արմատ՝ x_1,2=−(−6)±√16/2=6±4/2

Պատասխան՝ x₁=5,x₂=1

4) Հաշվենք 2x²−4x−3=0 հավասարման տարբերիչը՝ D=4²−4⋅(−3)⋅2=16+24=40>0 Հավասարումն ունի երկու արմատ՝ x_1,2=−(−4)±√40/2⋅2=4±√4⋅10/2=2±√10

Ուշադրություն

Եթե թվերն արմատի տակից դուրս չեն գալիս, դա չի նշանակում, որ հավասարումը լուծում չունի: Այդ դեպքում արմատներն իռացիոնալ թվեր են:

Առաջադրանքներ։

1․ Լուծել հավասարումները․

4x²-4x+1=0

D=4²+4⋅4⋅1=16+16=32>0

Հավասարումն ունի երկու արմատ՝ 

x_1,2=-4+√32/2⋅4=1,6/8

Պատասխան՝ x_1,2=0,2

2․Լուծել հավասարումները․

3․ Լուծել հավասարումները․

4․ Լուծել հավասարումները․

Պարապմունք 51

Թեմա՝ Պարզագույն իռացիոնալ անհավասարումներ։

Եթե անհավասարման անհայտը գտնվում է քառակուսի արմատի նշանի տակ, ապա  այդպիսի անհավասարումը անվանում են իռացիոնալ: 

Սովորենք լուծել պարզագույն իռացիոնալ հավասարումները: Պարզագույն իռացիոնալ անհավասարումներն են՝ √x<a և √x>a, որտեղ a -ն տրված իրական թիվ է:

Դիտարկենք √x<a անհավասարումը:

1) Եթե a≤0, ապա թվաբանական քառակուսի արմատի սահմանման համաձայն, անհավասարումը լուծում չունի:

2) Եթե a>0, ապա պետք է անհավասարումը բարձրացնել քառակուսի և պահանջել, որ արմատն իմաստ ունենա (արմատատակ թիվը լինի ոչ բացասական): Եկանք հետևյալ համակարգին՝

Որպես պատասխան ստանում ենք հետևյալ կրկնակի անհավասարումը՝ 0≤x<a²

Դիտարկենք √x>a անհավասարումը:

1) Եթե a<0, ապա ձախից ոչ բացասական թիվ է, իսկ աջից՝ բացասական: Անհավասարումը միշտ ճիշտ է, եթե արմատն իմաստ ունի:

Հետևաբար այս դեպքում անհավասարման պատասխանը ԹԱԲ -ն է՝ [0;+∞)

2) Եթե a≥0, ապա պետք է անհավասարումը բարձրացնել քառակուսի և պահանջել, որ արմատն իմաստ ունենա (արմատատակ թիվը լինի ոչ բացասական): Գալիս ենք հետևյալ համակարգին՝

Որպես պատասխան ստանում ենք հետևյալ անհավասարումը՝ x>a²

Նման ձևով վարվելով՝ կարելի է լուծել պարզագույն ոչ խիստ անհավասարումները:

√x ≤a անհավասարման դեպքում գալիս ենք հետևյալ եզրակացություններին:

1) Եթե a<0, լուծում չկա: 

2) Եթե a≥0, ապա x∈[0;a2]

√x ≥ a անհավասարման դեպքում գալիս ենք հետևյալ եզրակացություններին:

1) Եթե a<0, պատասխանը ԹԱԲ -ն է՝ [0;+∞)

2) Եթե a≥0, ապա x∈[a2;+∞)

Օրինակ

Լուծենք √2x−1<3 իռացիոնալ անհավասարումը:

1) Սկզբում գտնենք ԹԱԲ -ը՝ 2x−1≥0

2) Երկու մասերը բարձրացնենք քառակուսի՝ (√2x−1)²❤²

3) Եկանք հետևյալ համակարգին՝

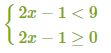
4) Լուծենք ստա`ցված համակարգը՝

5) Պատասխանը ստացված բազմությունների հատումն է՝ x∈[0.5;5)

Առաջադրանքներ։

1․Լուծել անհավասարումները;

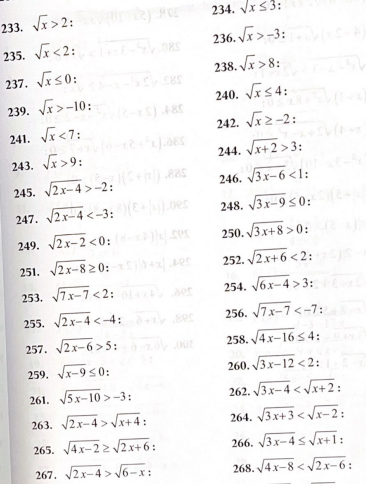
2․ Լուծել անհավասարումները։

Պարապմունք 50

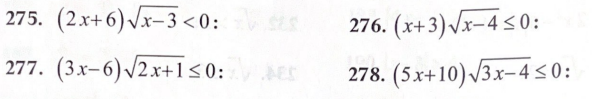
Թեմա` Պարզագույն իռացիոնալ հավասարումների լուժումը:

Եթե հավասարման անհայտը գտնվում է քառակուսի արմատի նշանի տակ, ապա այդպիսի հավասարումը անվանում են իռացիոնալ: 

Կյանքի շատ իրավիճակներ նկարագրվում են իռացիոնալ հավասարումներով: Ուստի, սովորենք լուծել գոնե պարզագույն իռացիոնալ հավասարումները:

Դիտարկենք 

Եթե հավասարման անհայտը գտնվում է քառակուսի արմատի նշանի տակ, ապա այդպիսի հավասարումը անվանում են իռացիոնալ: 

Կյանքի շատ իրավիճակներ նկարագրվում են իռացիոնալ հավասարումներով: Ուստի, սովորենք լուծել գոնե պարզագույն իռացիոնալ հավասարումները:

Դիտարկենք √2x+1=3 իռացիոնալ հավասարումը:

Ըստ քառակուսի արմատի սահմանման, այն նշանակում է, որ 2x+1=3²: Փաստորեն, քառակուսի բարձրացնելով, տրված իռացիոնալ հավասարումը բերեցինք 2x+1=9 գծային հավասարմանը:

Ուշադրություն

Քառակուսի բարձրացնելը իռացիոնալ հավասարումների լուծման հիմնական եղանակն է:

Դա բնական է, եթե պետք է ազատվել քառակուսի արմատի նշանից:

2x+1=9 հավասարումից ստանում ենք՝ x=4: Սա միաժամանակ  2х+1=9 գծային  և √2x+1=3  իռացիոնալ հավասարումների արմատն է:

Քառակուսի բարձրացնելու եղանակը տեխնիկապես բարդ չէ իրականացնել, սակայն երբեմն այն բերում է անցանկալի իրավիճակների:

Օրինակ

Դիտարկենք √2x−5=√4x−7 իռացիոնալ հավասարումը:

Երկու մասերը բարձրացնելով քառակուսի, ստանում ենք՝ (√2x−5)²=(√4x−7)² 2x−5=4x−7

Լուծելով ստացված 2x−4x=−7+5 հավասարումը, ստանում ենք x=1

Սակայն x=1, որը 2x−5=4x−7 գծային հավասարման արմատն է, չի բավարարում տրված իռացիոնալ հավասարմանը: Ինչո՞ւ: Իռացիոնալ հավասարման մեջ  փոխարեն տեղադրենք 1: Կստանանք՝ √−3=√−3

Հավասարումը բնականաբար չի բավարարվում, քանի որ հավասարության ձախ և աջ մասերը իմաստ չունե

Ստացել ենք ավելորդ արմատ: Այսպիսի իրավիճակներում ասում ենք, որ x=1 -ը թույլատրելի արժեք չէ, կամ չի պատկանում թույլատրելի արժեքների բազմությանը: Դուրս եկավ, որ այս դեպքում, իռացիոնալ հավասարումը արմատ չունի, մինչդեռ քառակուսի բարձրացնելուց ստացված գծային հավասարումը արմատ ուներ:

Պետք է այսպիսի ավելորդ արմատները ժամանակին հայտնաբերել և չընդգրկել լուծումների մեջ՝ դեն նետել: Դա արվում է ստուգման միջոցով: 

Իռացիոնալ հավասարումների համար, ստուգումը լուծման անհրաժեշտ փուլ է, որը օգնում է հայտնաբերել և դեն նետել ավելորդ արմատնելը: 

Ուշադրություն

Այսպիսով, իռացիոնալ հավասարումը լուծելու համար պետք է՝

1) այն բարձրացնել քառակուսի,

2) լուծել ստացված հավասարումը,

3) կատարել ստուգում՝ դեն նետելով ավելորդ արմատները,

4) գրել վերջնական պատասխանը:

Կիրառելով այս եզրակացությունը, դիտարկենք հետևյալ օրինակը:

Օրինակ

Լուծենք √5x−16=2 հավասարումը:

1) Երկու մասերը բարձրացնենք քառակուսի՝ (√5x−16)²=2²

2) Լուծենք ստացված հավասարումը՝

5x−16=4 5x=20 x=4

3) Կատարենք ստուգում: √5x−16=2 հավասարման մեջ տեղադրենք x=4: Ստանում ենք՝ √4=2 ճիշտ հավասարությունը:

4) Պատասխան՝ √5x−16=2 հավասարման լուծումը x=4 -ն է:

Հարցեր և առաջադրանքներ։

1․Ո՞ր հավասարումներն են կոչվում իռացիոնալ։

Եթե հավասարման անհայտը գտնվում է քառակուսի արմատի նշանի տակ, ապա այդպիսի հավասարումը անվանում են իռացիոնալ: 

2․ Ինչպե՞ս են լուծում պարզագույն իռացիոնալ հավասարումները։

քառակուսի բարձրացնելով

3․ Լուծել հավասարումները։

ա․ 9

զ․ -1

4․ Լուծել հավասարումները։

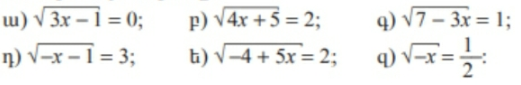
5․ Լուծել հավասարումները․

249․ 4

250․ 9

251․ 25

252․

253․

254․ 81

255․

Պարապմունք 49

Թեմա՝ Թվաբանական քառակուսի արմատների հատկությունները։

1․ Պարզեցնել արտահայտությունը․

ա) 5√2

բ) √2

գ) -4√a

դ)

ե)

զ) -√2

2․ Համեմատել արտահայտությունների արժեքները առանց արմատը հաշվելու։

ա) >

3․ Պարզեցնել արտահայտությունը․

4․ Հայտարարում ազատվել արմատանշանից։

5․ Կրճատել կոտորակը․

6․ Արտադրիչը տանել արմատանշանի տակ․

Պարապմունք 47

Թեմա՝ Թվաբանական քառակուսի արմատ։

Տրված a թվից թվաբանական քառակուսի արմատ կոչվում է այն ոչ բացասական թիվը, որի քառակուսին հավասար է տրված a թվին:

Նշանակում ենք այսպես՝ √a: Կարդում ենք՝ a թվից քառակուսի արմատ: 

a -ն թիվն անվանում են արմատատակ թիվ:  

√16=4, քանի որ՝ 4²=16

Ուշադրություն՝ Բացասական թվից քառակուսի արմատ գոյություն չունի:

Օրինակ ՝√-16 արտահայտությունն իմաստ չունի, քանի որ չկա այնպիսի a իրական թիվ, որի քառակուսին հավասար լինի բացասական թվի՝ a²≠−16

Քառակուսի արմատը գտնելու համար պետք է լավ իմանալ թվերի քառակուսիները:

Թվերի հաճախ օգտագործվող քառակուսիներ՝

Հետևաբար, √81=9; √121=11; √361=19 և այլն:

Ուշադրություն՝ √1=1,√0=0

Եթե արմատատակ թիվը տասնորդական կոտորակ է, ապա պետք է ուշադրություն դարձնել ստորակետից հետո եկող թվերի քանակի վրա:

√0,09=0,3; քանի որ 0,3²=0,3⋅0,3=0,09 √0,0016=0,04 √0,009= ?

Այս թիվը բանավոր հաշվել հնարավոր չէ, քանի որ այն անվերջ տասնորդական կոտորակ է:

Եթե արմատատակ թիվը վերջանում է զրոներով, ապա պետք է ուշադրություն դարձնել դրանց քանակի վրա

√400=20 √1210000=1100 √9000=?

Այս թիվը ևս բանավոր հաշվել հնարավոր չէ, քանի որ այն անվերջ տասնորդական կոտորակ է (ստուգիր հաշվիչի օգնությամբ):

Առաջադրանքներ։

1․ Հաշվել քառակուսի արմատը․

3, 4, 5, 7, 9, 11, 15, 17, 19, 24, 26, 22, 27, 31

2․ Հաշվել

ա․ 3

բ․ 9

գ․ 5

դ․ 9

ե․ 6

զ․ 2

է․ 4

ը․ 3

թ․ 1,3

3․ Հաշվել

ա․ 18

բ․ 10/3

գ․ 1

դ․ 1,2

ե․ 3/10

զ․ 0,7

է․ 3

ը․ 18/5

թ․ 5,2

4․ Համեմատել

ա․ 10>9

բ․ 10<11

գ․ 2<3

դ․ 1/5<0,5

5․ Հաշվել

6․ Հաշվել

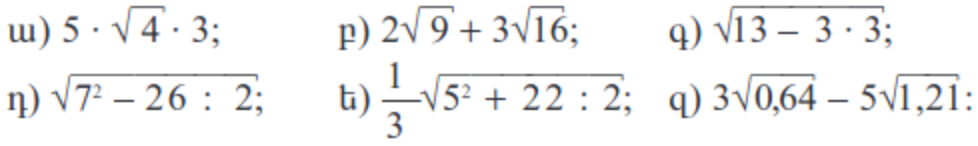
7․ Հաշվել

8․ Գտնել  արտահայտության արժեքը՝  0.4√0.16+1/2⋅√256

Պարապմունք 42

Թեմա՝ Մեկ անհայտով գծային անհավասարումների համակարգեր

Անհավասարումների համակարգը բաղկացած է մեկ կամ մի քանի անհավասարումներից: Այդ անհավասարումները միավորվում են ձևավոր փակագծով: Պետք է գտնել այդ անհավասարումների բոլոր ընդհանուր լուծումները: 

Փոփոխականի այն արժեքները, որոնց դեպքում համակարգի անհավասարումներից յուրաքանչյուրը վերածվում է ճիշտ անհավասարության, կոչվում են անհավասարությունների համակարգի լուծումներ: 

Գծային անհավասարումների համակարգը լուծելու համար, պետք է լուծել համակարգի յուրաքանչյուր անհավասարումը և այնուհետև գտնել ստացված լուծումների բազմությունների ընդհանուր մասը (հատումը): Դա էլ հենց կլինի համակարգի բոլոր լուծումների բազմությունը:

Լուծել համակարգը՝ նշանակում է գտնել նրա բոլոր լուծումները:

Օրինակ․

Լուծենք հետևյալ համակարգը՝ 

1. Լուծելով առաջին անհավասարումը, ստանում ենք՝

2x>4

x>2

2. Լուծելով երկրորդ անհավասարումը, ստանում ենք՝

3x<13

x<13/3

3. Ստացված միջակայքերը նշենք թվային առանցքի վրա: Յուրաքանչյուրի համար ընտրենք իր նշումը:

4. Անհավասարումների համակարգի լուծումը թվային առանցքի վրա նշված երկու բազմությունների հատումն է:

Մեր դեպքում ստանում ենք այս պատասխանը՝ (2;13/3)

Առաջադրանքներ․

1. Կոորդինատային ուղղի վրա նշեք անհավասարումների համակարգի բոլոր լուծումները (եթե դրանք գոյություն ունեն)․

ա)

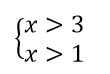
X-ը պատկանում է (3; + անվերջություն)

բ)

X-ը պատկանում է (1; + անվերջություն)

գ)

X-ը պատկանում է (2; – անվերջություն)

դ)

X-ը պատկանում է (-5; – անվերջություն)

ե)

X-ը պատկանում է (-7; – 5)

զ)

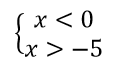
X-ը պատկանում է (-5; 0)

2․Փակագծերում նշված թիվը հանդիսանո՞ւմ է արդյոք անհավասարումների համակարգի լուծում՝

ա)

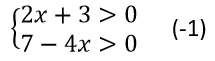
այո

բ)

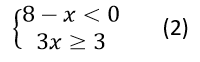
ոչ

3․Լուծել անհավասարումների համակարգը

4․Լուծել անհավասարումների համակարգը․

ա)

բ)

գ)

դ)

5․Լուծել անհավասարումների համակարգը

ա)

բ)

գ)

դ)

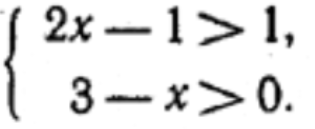
ե)

զ)

Պարապմունք 39

Թեմա՝ Առաջին աստիճանի մեկ անհայտով անհավասարումներ։

kx−b>0 կամ kx−b<0 տեսքի անհավասարումները, որտեղ k -ն և b -ն տրված թվեր են, ընդ որում k≠0, անվանում են առաջին աստիճանի մեկ x անհայտով անհավասարումներ:Օրինակ՝ 2 +>0,3-<0

k-ն անհավասարման անհայտի գործակից, իսկ b-ն ազատ անդամ։

Անհավասարման լուծումը այն թիվն է, որը x-ի փոխարեն տեղադրելով ստացվում է ճիշտ թվային անհավասարություն։

Լուծել անհավասարումը նշանակում է, գտնել նրա բոլոր լուծումները, կամ ապացուցել, որ դրանք չկան։

Օրինակ 1․ a−5<0, a<5 Պատասխան՝a∈(-∞;5)

Օրինակ 2․ −2y−100<0 Երկու մասը բաժանելով -2-ի, կստանանք՝
y>−50 (անհավասարության նշանը փոխվում է)
Պատասխան՝y∈(−50;+∞)

Հուշում՝ երբ թիվը կամ փոփոխականը անհավասարման մի մասից տեղափոխվում է մյուս մասը, ապա նրա նշանը փոխվում է:

Մեկ անհայտով առաջին աստիճանի անհավասարումների լուծման ալգորիթմը հետևյալն է՝ ա այդ անհավասարման ազատ անդամը տեղափոխում ենք անհավասարման աջ մասը, փոխելով նշանը հակադիրով, բ ստացված անհավասարման երկու մասը բաժանել անհայտի գործակցի վրա, ընդ որում, եթե >0, ապա անհավասարման նշանը չի փոխվում, իսկ եթե<0, ապա անհավասարման նշանը փոխվում է հակադիրով։ Ստացված անհավասարումը հենց պատասխանն է։

Հարցեր և առաջադրանքներ։

1․ Ի՞նչն են անվանում առաջին աստիճանի մեկ անհայտով անհավասարում։ Գրել մի քանի օրինակ։

2․ Ի՞նչն են անվանում առաջին աստիճանի մեկ անհայտով անհավասարման լուծում։

3․ Ի՞նչ է նշանակում լուծել առաջին աստիճանի մեկ անհայտով անհավասարումը։

4․ Արդյո՞ք 4 թիվը հանդիսանում է նշված անհավասարման լուծում՝ ա) x>0 բ) x<-2 գ) -4<x<4 դ) x<4,2 ե) 3,8 <x<4,1

5․ Լուծել անհավասարումները․

6․ Լուծել անհավասարումները և լուծումը պատկերել թվային ուղղի վրա․

7․ Լուծել անհավասարումները և լուծումը պատկերել թվային ուղղի վրա․

8․ Լուծել անհավասարումները․

9․ Լուծել անհավասարումները․

10․ Լուծել անհավասարումները․

11․ Լուծել անհավասարումները․

Պարապմունք 37

Թեմա՝ Թվային միջակայքեր թվային ուղղի վրա։

Գիտենք, որ իրական թվերի երկրաչափական մոդելը թվային ուղիղն է: Ցանկացած իրական թիվ թվային ուղղի վրա ունի իր դիրքը: Հիմա կպարզենք, թե ինչպես են թվային ուղղի վրա պատկերվում թվային միջակայքերը: Կօգտագործենք հետևյալ նշանակումները. 

Անհավասարությունների և ծայրակետերի նշանակումներ	Բազմությունների նշանակումներ
≤ կամ ≥ • (ծայրակետն ընդգրկված է)	[ և] քառակուսի փակագծեր
< կամ > о (ծայրակետն ընդգրկված չէ)	( և ) կլոր փակագծեր

Գոյություն ունեն թվային ուղղի վրա բազմությունների 4 տեսակի նշանակումներ:

Ամբողջ թվային ուղիղը նշանակվում է այսպես՝ (−∞;∞)

Բաց և փակ միջակայքեր թվային առանցքի վրա

Արդեն դիտարկել ենք թվային ուղղի վրա որոշ բազմությունների նշանակումը՝ (−∞;∞),(a;+∞),[a;+∞),(−∞;a],(−∞;a)

Սրանք, այսպես կոչված, անսահմանափակ բազմություններ (մի կողմից կամ երկու կողմից) են: Դիտարկենք սահմանափակ բազմություններ թվային առանցքի վրա:

Եթե x թիվը միաժամանակ բավարարում է x>−4 և x<5 անհավասարություններին, ապա այն բավարարում է −4<x<5 երկկողմանի անհավասարությանը:

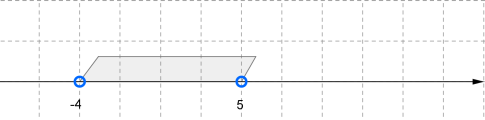
−4<x<5 երկկողմանի անհավասարությանը բավարարող բոլոր թվերի բազմությունը անվանում են թվային միջակայք և նշանակում են այսպես՝ (−4;5):

Միջակայքը պատկերենք թվային ուղղի վրա: Կարդում ենք՝ «−4, 5 ինտերվալ», կամ «բաց միջակայք» : Նկատենք, որ հատվածի ծայրակետերը ընդգրկված չեն (սևացված չեն):

Դիտարկենք ուրիշ միջակայքեր:

−4≤x≤5 կամ x∈[−4;5]: Կարդում ենք՝ «−4, 5 հատված», կամ «փակ միջակայք»: Նկատենք, որ հատվածի ծայրակետերը ընդգրկված են (սևացված են):

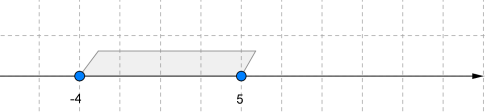
−4≤x<5 կամ x∈[−4;5): Կարդում ենք՝ «−4, 5 կիսաինտերվալ», կամ «կիսաբաց միջակայք»: Նկատենք, որ կիսաինտերվալի ծայրակետերից մեկը՝ −4 -ը ընդգրկված է (սևացված է), իսկ մյուսը՝ 5 -ը ընդգրկված չէ (սևացված չէ):

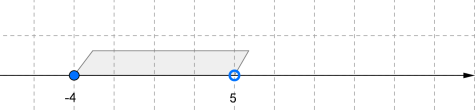
−4<x≤5 կամ x∈(−4;5]: Սա ևս կիսաինտերվալ է՝ բաց ձախ ծայրակետով:

x-երի առանցքի a և b կետերից և նրանց միջև գտնվող բոլոր կետերից բաղկացած բազմությունն անվանում են a-ից b հատված և նշանակում՝ [a;b]:

Հարցեր և առաջադրանքներ:

1. Ո՞ր թվեր են պատկանում տրված միջակայքին՝ (−∞;−5)

ա) -6 բ) 1 գ) 5 դ) -1 ե) 20 զ) 10 է) -10 թ) -9

2. Պարզել՝ ճիշտ է, թե սխալ հետևյալ պնդումը՝ −12∈(−12;7]

ա) սխալ է  բ) ճիշտ է

3. Ո՞ր թվեր են պատկանում տրված հատվածին՝ [−12;0]

ա) −9  բ) −10 գ) 20  դ) −6  ե) −1 զ) 10  է)1   թ)5

4. Ո՞ր թվերը չեն պատկանում այս միջակայքին՝ (−1;10)

  ա) 12  բ) 1  գ) 10  դ) −1   ե) 5  զ) 2

5. Ընտրիր x∈(−∞;−1] միջակայքի պատկերը թվային առանցքի վրա, եթե a=−1

• 
• Ճիշտ է
• 
• 

6.Գրառել նշանակումը՝

ա)

բ)

գ)

դ)

ե)

զ)

է)

ը)

7. Կարդալ թվային բազմության անվանումը և այն պատկերել այն կոորդինատային ուղղի վրա՝]

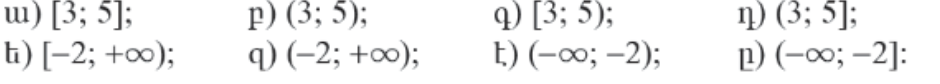
ա) x∈[3;5]

բ) x∈(3;5)

գ) x∈[3;5)

դ) x∈(3;5]

ե) x∈[-2;+∞)

զ) x∈(-2;+∞)

է) x∈(-∞;-2]

ը) x∈(-∞;-2)

8․ Թվարկել թվային բազմությանը պատկանող բոլոր ամբողջ թվերը․

9․ Կոորդինատային առանցքի վրա նշել այն թվերը, որոնք՝

10․Անվանել թվային բազմությանը պատկանող չորս ամբողջ թվեր՝

ա) 3, 4, 5 բ) 6, 7, 8 գ) -1, -2, -3 դ) -7, -8, -9

11․Գրառել նկարում պատկերված բազմությունները՝

ա) x∈[3;7]

բ) x∈(3;7)

գ) x∈(5;6]

դ) x∈[5;6)

ե) x∈[7;+∞)

զ) x∈(+∞;8)

է) x∈(7;+∞)

ը) x∈(+∞;8]

Պարապմունք 36

Թեմա՝ Թվային արնհավասարությունների հատկությունները:

a>b և c>d կամ  a<b և c<d անհավասարությունները (միևնույն նշանի) կոչվում են միանուն:

a>b և c<d կամ  a<b և c>d անհավասարությունները (հակառակ նշանի) կոչվում են հականուն:

Օրինակ

6>−5 և 25>17 անհավասարությունները միանուն են, իսկ -41<−5 և 36>17 անհավասարությունները՝ հականուն:

Անհավասարությունների գումարումը

Եթե a>b և c>d, ապա a+c>b+d

Միանուն անհավասարությունները կարելի է գումարել :

Օրինակ՝ Ունենք երկու անհավասարություն՝ 5<10 և 4<9, գումարելով անհավասարության երկու մասերը, կստանաք՝ 5+4<10+9, 9<19։

Եթե a−ն,b−ն,c−ն,d−ն դրական թվեր են և a>b, c>d, ապա ac>bd

Եթե դրական ձախ և աջ մասերով միանուն անհավասարությունները բազմապատկենք, ապա կստացվի միանուն անհավասարություն (նշանը չի փոխվի):

Անհավասարության աստիճան բարձրացնելը

Եթե a և b թվերը դրական են a<b, ապա aⁿ<bⁿ, որտեղ n -ը բնական թիվ է:  
Եթե դրական ձախ և աջ մասերով միանուն անհավասարումները բարձրացնել միևնույն բնական աստիճանի, ապա կստացվի միանուն անհավասարություն (նշանը չի փոխվի):

Օրինակ՝  Քանի, որ 2<3, ապա քառակուսի բարձրացնելով, ստանում ենք ևս մեկ ճիշտ անհավասարություն՝  2²=4,  3²=9, 4<9

Առաջադրանքներ։

1․Գումարել թվային անհավասարությունները։

ա) 18>11 և 15>7  33>18 

բ) -4>-6 և 13>8    9>2

գ) -16<-7 և 12<37   -4<30

դ) -9<0 և 5<19   -4<19

2. Գումարել թվային անհավասարությունները։

ա) 24>20

բ) 1>-1

գ) -4<-2

դ)  0<9

3․Բազմապատկել թվային արտահայտությունները։

ա) 14>10 և 2>1  28>10

բ) 5>3 և 6>5  30>15

գ) 6<7 և 2<3   12<21

դ) 8<9 և 1<2   8<18

4․Գումարել  անհավասարությունները: 

ա) 22>17 և 3.2>0.6  25.2>17.6

բ) 53<65 և 7,6<10,9   60.6<75.9

5․Զբոսաշրջիկ առաջին օրն անցավ 20 կմ-ից ավելի, իսկ երկրորդ օրը 25 կմ-ից ավելի։ Արդյո՞ք կարելի պնդել, որ զբոսաշրջիկն անցել է 45 կմ-ից ավելի ճանապարհ։ Պատասխանը հիմնավորել։

a>20

b>25

a+b>45

6․ Ուղղանկյան երկարությունը 13 սմ-ից փոքր է, իսկ լայնությունը՝ 5 սմ-ից փոքր։Արդյո՞ք կարելի պնդել, որ ուղղանկյան մակերեսը 65 սմ²-ից ավելի է։ Պատասխանը հիմնավորել։

a<13

b<5

a x b > 65